递归 | 悦来客栈

今天在看leetcode上的顺序链表合并的问题时，又一次对递归的问题进行了思考。算法图解上的盒子与钥匙的例子确实生动的表述了循环和递归在解决具体问题时的不同思考方式，但是还是觉得差了点意思。

递归

递归是很多算法都使用的一种编程方法，连我一个外行都能感觉到这种思维方式的简洁和优美，唯一的问题就是自己写不出来~

下面是我在知乎上看到的一篇大神的文章：帅地。让我对递归的理解更加深入，非常感谢。

1.递归的三大要素

以阶乘的计算为例：

第一要素：明确你这个函数想要干什么

对于递归，我觉得很重要的一个事就是，这个函数的功能是什么，他要完成什么样的一件事，而这个，是完全由你自己来定义的。也就是说，我们先不管函数里面的代码什么，而是要先明白，你这个函数是要用来干什么。

例如，我定义了一个函数

// 算 n 的阶乘(假设n不为0)
int f(int n){

}

这个函数的功能是算 n 的阶乘。好了，我们已经定义了一个函数，并且定义了它的功能是什么，接下来我们看第二要素。

第二要素：寻找递归结束条件

所谓递归，就是会在函数内部代码中，调用这个函数本身，所以，我们必须要找出递归的结束条件，不然的话，会一直调用自己，进入无底洞。也就是说，我们需要找出当参数为啥时，递归结束，之后直接把结果返回，请注意，这个时候我们必须能根据这个参数的值，能够直接知道函数的结果是什么。

例如，上面那个例子，当 n = 1 时，那你应该能够直接知道 f(n) 是啥吧？此时，f(1) = 1。完善我们函数内部的代码，把第二要素加进代码里面，如下

// 算 n 的阶乘(假设n不为0)
int f(int n){
    if(n == 1){
        return 1;
    }
}

有人可能会说，当 n = 2 时，那我们可以直接知道 f(n) 等于多少啊，那我可以把 n = 2 作为递归的结束条件吗？当然可以，只要你觉得参数是什么时，你能够直接知道函数的结果，那么你就可以把这个参数作为结束的条件，所以下面这段代码也是可以的。

// 算 n 的阶乘(假设n>=2)
int f(int n){
    if(n == 2){
        return 2;
    }
}

注意我代码里面写的注释，假设 n >= 2，因为如果 n = 1时，会被漏掉，当 n <= 2时，f(n) = n，所以为了更加严谨，我们可以写成这样：

// 算 n 的阶乘(假设n不为0)
int f(int n){
    if(n <= 2){
        return n;
    }
}

所以：结束条件也可以理解为，“递”这一过程的尽头。

第三要素：找出函数的等价关系式

我本来只是把这一步当做修改参数范围，仔细想想还是浅了。其本质就是通过寻找函数的等价关系式来缩小参数范围的。

第三要素就是，我们要不断缩小参数的范围，缩小之后，我们可以通过一些辅助的变量或者操作，使原函数的结果不变。

例如，f(n) 这个范围比较大，我们可以让 f(n) = n * f(n-1)。这样，范围就由 n 变成了 n-1 了，范围变小了，并且为了原函数f(n) 不变，我们需要让 f(n-1) 乘以 n。

说白了，就是要找到原函数的一个等价关系式，f(n) 的等价关系式为 n f(n-1)，即f(n) = n f(n-1)，写进函数里。如下：

// 算 n 的阶乘(假设n不为0)
int f(int n){
    if(n <= 2){
        return n;
    }
    // 把 f(n) 的等价操作写进去
    return f(n-1) * n;
}

至此，递归三要素已经都写进代码里了，所以这个 f(n) 功能的内部代码我们已经写好了。这就是递归最重要的三要素，每次做递归的时候，你就强迫自己试着去寻找这三个要素。

实际上，如果只看这个函数的功能，其实就是执行的一个乘法运算嘛。真正的执行流程为：

第一步递进，递进的过程其实就是在寻找让递进结束的那个返回值。找到后递进终止。

第二部回归，通过递进得到的返回值再结合等价关系式，得到了倒数第二级的返回值，再结合等价关系式，又能得到倒数第三级的返回值。。。最终回归到函数第一级：f(n)的返回值。

2.实例

案例1：小青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

递归函数功能

定义f(n)，功能是求青蛙跳上一个n级的台阶总共有多少种跳法
结束条件

n = 1时，很明显，返回1
关系式

有点麻烦，最开始的想法：f(n) = f(n-1)+1..。我可能真的是个傻子。

实际上，最后一次跳跃到n阶上是有两种可能的，一阶或者两阶。

所以：f(n) = f(n-1)+f(n-2)

代码就这么轻而易举的得到了

int f(int n){
    if(n == 1){
        return 1;
    }
    ruturn f(n-1) + f(n-2);
}

但是好像不太对吧，当n = 2时，返回值为f(1)+f(0)，此时的f(0)避开了我们的限制条件，死循环就此诞生！！

这里就出现了一个新的问题：递归结束条件是否足够严谨

有很多人在使用递归的时候，由于结束条件不够严谨，导致出现死循环。也就是说，当我们在第二步找出了一个递归结束条件的时候，可以把结束条件写进代码，然后进行第三步，但是请注意，当我们第三步找出等价函数之后，还得再返回去第二步，根据第三步函数的调用关系，会不会出现一些漏掉的结束条件。就像上面，f(n-2)这个函数的调用，有可能出现 f(0) 的情况，导致死循环，所以我们把它补上。代码如下：

int f(int n){
    //经过分析，f(2)=2也是一个临界条件。
    if(n <= 2){
        return n;
    }
    ruturn f(n-1) + f(n-2);
}

案例3：反转单链表

反转单链表。例如链表为：1->2->3->4。反转后为 4->3->2->1

1、定义递归函数功能

假设函数 reverseList(head) 的功能是反转单链表，其中 head 表示链表的头节点。代码如下：

1 2	Node reverseList(Node head){ }

2. 寻找结束条件

当链表只有一个节点，或者如果是空表的话，你应该知道结果吧？直接啥也不用干，直接把 head 返回呗。代码如下：

Node reverseList(Node head){
    if(head == null || head.next == null){
        return head;
    }
}

3. 寻找等价关系

这个的等价关系不像 n 是个数值那样，比较容易寻找。但是我告诉你，它的等价条件中，一定是范围不断在缩小，对于链表来说，就是链表的节点个数不断在变小，所以，如果你实在找不出，你就先对 reverseList(head.next) 递归走一遍，看看结果是咋样的。例如链表节点如下:

head->1——2——3——4

reverselist(head.next)的结果应该是：

head->4——3——2

这时候再来看 reverseList(head) 和 reverseList(head.next) 两个关系式的关系：
执行完 reverseList(head.next) 后，再将2.next = 1，再将1.next = null

代码就这样得到了：

Node reverseList(Node head){
    if(head == null || head.next == null){
        return head;
    }
    Node newList = reverseList(head.next);
    head.next.next = head;
    head.next = null;
    return newList;
}

3. 递归的优化思路

3.1考虑是否重复计算

告诉你吧，如果你使用递归的时候不进行优化，是有非常非常非常多的子问题被重复计算的。啥是子问题？ f(n-1),f(n-2)….就是 f(n) 的子问题了。
例如对于案例2那道题，f(n) = f(n-1) + f(n-2)。递归调用的状态图如下：

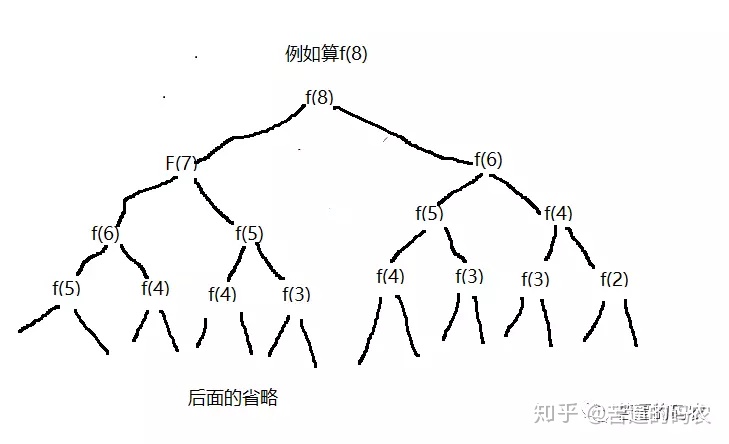
看到没有，递归计算的时候，重复计算了两次 f(5)，五次 f(4)。。。。这是非常恐怖的，n 越大，重复计算的就越多，所以我们必须进行优化。

如何优化？一般我们可以把我们计算的结果保证起来，例如把 f(4) 的计算结果保证起来，当再次要计算 f(4) 的时候，我们先判断一下，之前是否计算过，如果计算过，直接把 f(4) 的结果取出来就可以了，没有计算过的话，再递归计算。

用什么保存呢？可以用数组或者 HashMap 保存，我们用数组来保存把，把 n 作为我们的数组下标，f(n) 作为值，例如 arr[n] = f(n)。f(n) 还没有计算过的时候，我们让 arr[n] 等于一个特殊值，例如 arr[n] = -1。

当我们要判断的时候，如果 arr[n] = -1，则证明 f(n) 没有计算过，否则， f(n) 就已经计算过了，且 f(n) = arr[n]。直接把值取出来就行了。代码如下：

// 我们实现假定 arr 数组已经初始化好的了。
int f(int n){
    if(n <= 1){
        return n;
    }
    //先判断有没计算过
    if(arr[n] != -1){
        //计算过，直接返回
        return arr[n];
    }else{
        // 没有计算过，递归计算,并且把结果保存到 arr数组里
        arr[n] = f(n-1) + f(n-1);
        reutrn arr[n];
    }
}

也就是说，使用递归的时候，必要须要考虑有没有重复计算，如果重复计算了，一定要把计算过的状态保存起来。

3.2考虑是否可以自底向上

对于递归的问题，我们一般都是从上往下递归的，直到递归到最底，再一层一层着把值返回。

不过，有时候当 n 比较大的时候，例如当 n = 10000 时，那么必须要往下递归10000层直到 n <=1 才将结果慢慢返回，如果n太大的话，可能栈空间会不够用。

对于这种情况，其实我们是可以考虑自底向上的做法的。例如我知道

f(1) = 1;

f(2) = 2;

那么我们就可以推出 f(3) = f(2) + f(1) = 3。从而可以推出f(4),f(5)等直到f(n)。因此，我们可以考虑使用自底向上的方法来取代递归，代码如下：

public int f(int n) {
       if(n <= 2)
           return n;
       int f1 = 1;
       int f2 = 2;
       int sum = 0;

       for (int i = 3; i <= n; i++) {
           sum = f1 + f2;
           f1 = f2;
           f2 = sum;
       }
       return sum;

这种方法，其实也被称之为递推。